¿Pueden las matemáticas ayudarnos a elegir al mejor candidato? Por Clara Grima
- Cómo las matemáticas nos pueden ayudar a tomar mejores decisiones a la hora de elegir candidatos... o cajas sorpresa
- Una matemática viene a verte: Todos los miércoles, en La 2 a las 19:45 horas | Disponible en RTVE Play


Existen personas que se conforman con la primera oferta, temiendo que las que vengan sean peores. Otras, en cambio, rechazan cualquier proposición porque esperan siempre una mejor. ¿Nos pueden ayudar las matemáticas a elegir bien?
A menudo tenemos la tentación de conformarnos con las primeras ofertas movidos por el miedo a que lo que vendrá después sea peor. O todo lo contrario. Nos dedicamos a rechazar proposiciones esperando que la final sea la mejor. Porque si no, no sería la final, como decían en aquella película, El exótico hotel Marigold.
Pues bien, ni una cosa ni otra. Existe un método clásico empleado en teoría de decisión, conocido con el sexista nombre del problema de la secretaria, y que vamos a renombrar como el problema del candidato, que nos enseña a tomar decisiones de forma inteligente descartando, con criterio, parte de lo bueno conocido.
Así que comprueben que sus cinturones están abrochados, su asiento en posición vertical y su mesita plegada porque ¡van a alucinar! Al menos, yo alucino con este problema y espero que también os provoque turbulencias y alguna sonrisa de sorpresa.
Si son seguidores de Una matemática viene a verte, recordarán que la semana pasada explicamos el problema de Monty Hall en dicho programa. Hoy vamos a presentar un concurso parecido (de hecho es parte del mismo proceso que se llevaba a cabo en Un, dos, tres).
Estamos en un concurso. Se nos presentan un cierto número de cajas, N, N cajas. Podemos abrirlas en el orden que nos plazca. Cada caja contiene una cantidad de dinero distinta de las otras (no sabemos qué cantidades hay en cada caja, ni cuáles son esas cantidades). Cada vez que abrimos una caja decidimos (después de contar el dinero en ella, se entiende) si nos quedamos con ella (esa es la caja que escogemos) o si la descartamos para siempre (una vez que una caja ha sido descartada, ya no podemos volver a ella). Tratamos de diseñar una estrategia que nos garantice escoger la caja con más dinero, con la probabilidad más alta posible.
¿A qué parece que no va a ser posible?
Empecemos con solo 3 cajas: A, B y C. Abrimos la primera (la A), como no tenemos ni idea de qué cantidades hay en las otras dos cajas, en A puede estar el mayor botín o no, no tenemos ninguna información adicional. Por lo tanto, si escogemos A, la probabilidad de acertar con el premio máximo es de ¿.
¿Podemos mejorar dicha estrategia?¿Podemos diseñar otra estrategia que garantice siempre más de ¿ de posibilidades de obtener la máxima cantidad?
Os propongo una: abrimos la primera caja (la A) y contamos el dinero que hay, pero la descartamos independientemente de cuánto dinero encierre. Ahora abrimos la segunda caja (la B), si contiene más dinero que la A, nos quedamos con la B. En caso contrario nos quedamos con la C. ¿En cuántos casos hemos acertado con esta estrategia?
Realicemos un examen viendo todas las posibilidades distintas. En cada caso, escribiremos las tres cajas ordenadas por la cantidad de dinero que tienen de mayor a menor.
El primer caso lo escribimos como (A, B,C) (esto es, la caja A tiene más dinero, después la B, después la C). Vamos a suponer, por simplificar, que las 3 cantidades son, respectivamente, 100, 50 y 25, pero, claro, eso no lo sabe el concursante a priori, no sabe cuál es el premio máximo. Pero lo pensamos así para hacer una simulación de los 6 casos posibles con 3 cajas.
Siguiendo la estrategia descrita, abrimos la A, la descartamos, abrimos la B y como tiene menos que la A, escogemos la C, que es la que menos dinero tiene. Mal empezamos. Nos hemos quedado con el peor premio.
Vamos a ver todos los casos usando las figuras que vienen a continuación. Para cada simulación, en otro color ponemos la caja que escogeremos con esta estrategia. Si el color es verde, es que hemos ganado.
Veamos, entonces, apoyándonos en las figuras, qué caja escogeríamos, en cada caso, siguiendo nuestra estrategia.
Para (A,B,C), es la que acabamos de explicar, escogemos C y hemos perdido.

Estrategia de toma de decisiones con matemáticas - Ejemplo1 RTVE
Si la situación fuera (A,C,B), despreciaríamos la B por tener menos que A, escogemos C, y también perdemos. Recuerda que abrimos las cajas por orden alfabético.

Estrategia de toma de decisiones con matemáticas - Ejemplo 2 RTVE
Si la distribución de los premios fuera (B,A,C), abrimos la A, la descartamos, abrimos la B que tiene más dinero y nos quedamos con ella y hemos ganado.

Estrategia de toma de decisiones con matemáticas - Ejemplo 2 RTVE
Para (B,C,A), escogemos la B y ganamos. ¡Ole!

Estrategia de toma de decisiones con matemáticas - Ejemplo 4 RTVE
Si la distribución de premios es (C,A,B), abrimos A y la descartamos, como B tiene menos dinero que A, también la descartamos y escogemos C. Ganamos otra vez.

Estrategia de toma de decisiones con matemáticas - Ejemplo 5 RTVE
Pero si la distribución de premios es (C,B,A), escogemos B y perdemos.

Estrategia de toma de decisiones con matemáticas - Ejemplo 6 RTVE
Como vemos, con esta estrategia, podemos garantizar un éxito del 50% (ganamos 3 veces de 6), lo cual es mejor que el 33% (=1/3) que teníamos si escogemos una caja al azar.
¿Qué? ¿Cómo os quedáis? Lo curioso es que esta estrategia se puede aplicar a cualquier número de cajas, por sorprendente que parezca y aunque no se conseguirá siempre un éxito del 50%, sí que podemos obtener un porcentaje sorprendentemente alto (mayor de ¿ independientemente del número de cajas). Sí, sí, éxito con una probabilidad casi del 37%, sea cual sea el número de cajas.
Se puede demostrar que el método que nos garantiza mejor resultado es el siguiente: Si tenemos que escoger entre N cajas, abrimos unas cuantas (digamos r) y las descartamos, pero anotamos de esas r cajas cuánto dinero tenía la que más tenía. A continuación seguimos abriendo las cajas restantes y nos quedamos con la primera que tenga más dinero que el que habíamos anotado como el máximo de las r primeras. Si ninguna tiene más dinero obviamente nos quedamos con la última.
Solo queda por determinar cuánto vale r, es decir, ¿cuántas cajas tenemos que abrir y descartar inicialmente?
Hemos visto que en el caso de 3 cajas (N=3, 3 cajas), r es 1, descartamos la primera tenga lo que tenga. Se puede comprobar que en el caso de N=4 (cuatro cajas), r también vale 1 (miramos la primera, la descartamos, y después vamos abriendo las restantes y nos plantamos si una tiene más dinero que la inicial, con esta técnica en el caso de 4 cajas podemos garantizar que escogeremos la mejor en un 46% de los casos).
En la siguiente tabla se muestra cuántas cajas tenemos que desestimar dependiendo del número de cajas que tengamos en total para asegurar la mayor probabilidad de éxito (se puede comprobar haciendo algunas cuentas, bastantes):
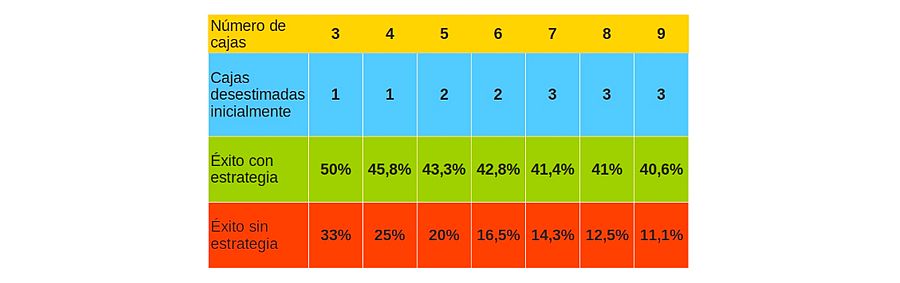
Estrategia de toma de decisiones con matemáticas RTVE
¿Y si son más de 9 cajas?
Se puede aplicar la misma técnica, pero ¿cómo calculamos el número de cajas, r, que tenemos que desestimar? Hay una regla más o menos sencilla: el número r de cajas a desestimar es el número entero más próximo a N/e donde e es el número de Euler, que es aproximadamente igual a 2,71828182845905 (no es un número racional y por tanto tiene infinitas cifras decimales que no se repiten de forma periódica).
Sí, yo también me quedé con esa cara cuando lo leí. Es alucinante. Pues sí, desechando ese número de cajas, podemos asegurar que la probabilidad de éxito es, por lo menos, 1/e. Es decir, tenemos asegurado el éxito en un 36,8% de los casos, por muy grande que sea el número de cajas. La tabla anterior añadiendo una fila con los valores obtenidos al dividir el número de cajas entre e, quedaría:
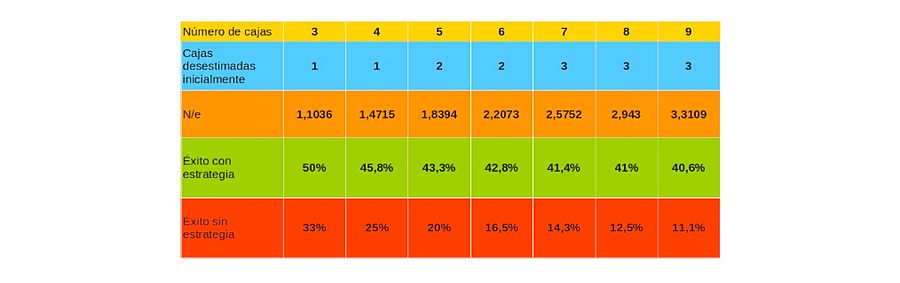
Estrategia de toma de decisiones con matemáticas RTVE
Os recuerdo que el número de cajas a desestimar es el entero (sin decimales) más cercano a N/e. Por eso, por ejemplo, con 7 cajas hay que descartar 3. Porque 7/e=2,5752, que está más cerca de 3 que de 2.
Otro ejemplo, para 10000 cajas, N=10000, tendríamos 10000/e= 3678,794411714, descartamos las 3679 (éste es el número entero más próximo a 3678,794411714) primeras cajas, y nos quedamos con la primera de las restantes que supere en dinero a todas las 3879 descartadas inicialmente y … ¡Tachán! ¡La probabilidad de éxito es del 37%!
Por Euler, ¿no os parece maravilloso y sorprendente? Podríamos pensar en usar esta estrategia para elegir a un candidato. Contamos cuántos hay en total, descartamos los que toquen según la fórmula que hemos usado, y nos quedamos con el primero que supere a los ya descartados.

Clara Grima y Pablo Simón en un momento de la grabación de 'Una matemática viene a verte' en el Senado RTVE
Aunque, honestamente, no creo que sea un buen método para elegir a qué partido votar. Al fin y al cabo, no son tantos. Y sí podemos saber cuánto encierran en la caja leyendo su programa.
De elecciones y matemáticas electorales hablamos en Una matemática viene a verte, con Pablo Simón, politólogo y profesor titular en la universidad Carlos III de Madrid, y Victoriano Ramírez, catedrático de Matemática Aplicada en la Universidad de Granada.
* Puedes disfrutar del programa Una matemática viene a verte cada miércoles a las 19:45 horas en La 2 y siempre, cuando quieras -gratis y online- en Una matemática viene a vertemiércoles a las 19:45 horasLa 2RTVE Play.

 Una matemática viene a verte
Una matemática viene a verte 




