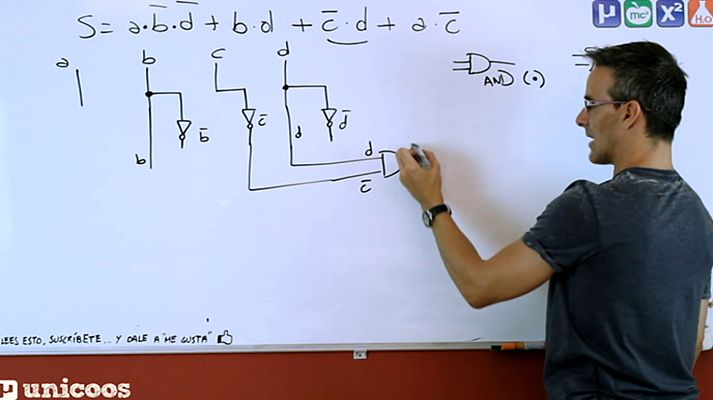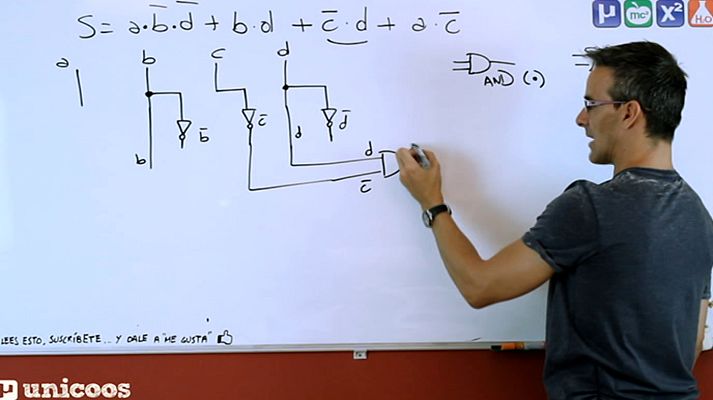14/16 - Ciencias Naturales
34
En esta franja horaria, nos acercaremos al tema de la electrónica digital y las funciones lógicas. Alternaremos estos contenidos con otros...
Disponible hasta 21-06-2020
15/05/2020 00:59:20