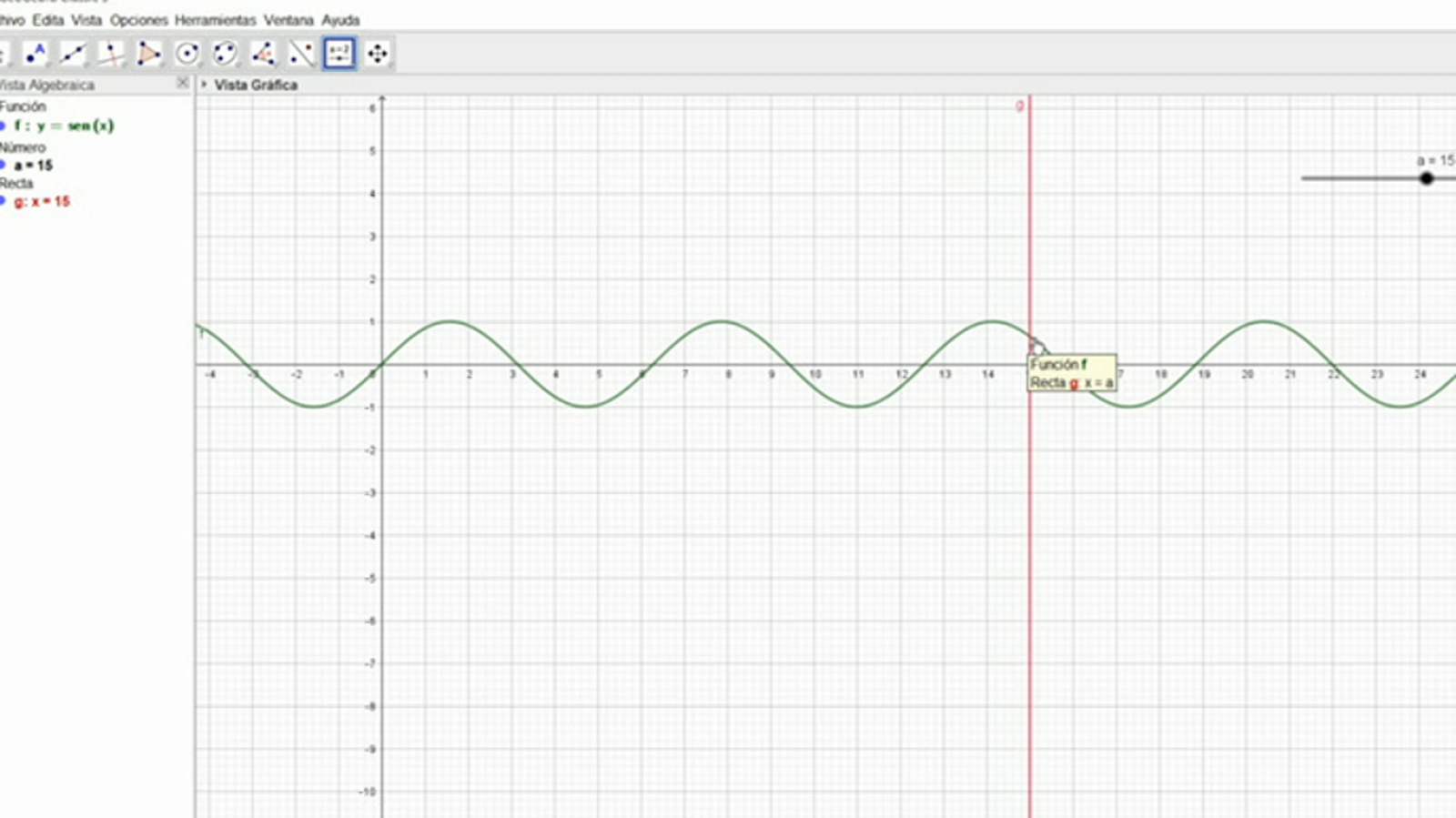
De 12 a 14 años - Matemáticas: álgebra y funciones
Vídeos sobre: álgebra (lectura de una expresión algebraica, monomios y polinomios); funciones (gráficas, afines, lineales).
Disponible hasta 21-06-2020
13/04/2020 01:00:44